Os 10 Melhores Exercícios Sobre Sistemas Lineares Com O Gabarito! – Beduka – Os 10 Melhores Exercícios Sobre Sistemas Lineares Com O Gabarito!
-Beduka: embarque nesta jornada fascinante pelo universo dos sistemas lineares! Descubra a elegância e a potência dessas ferramentas matemáticas, capazes de modelar situações complexas do mundo real, desde misturas químicas até o equilíbrio de forças em estruturas. Prepare-se para dominar os conceitos fundamentais, desde a definição de sistemas lineares e seus tipos até a resolução eficiente por meio de métodos como escalonamento e a regra de Cramer.
Através de exemplos práticos e exercícios cuidadosamente selecionados, você desenvolverá a habilidade de solucionar problemas, interpretando resultados e aplicando esse conhecimento em diversas áreas.
Aprender sistemas lineares é como aprender a decifrar uma linguagem secreta. Uma linguagem que descreve relações entre grandezas, permitindo a modelagem precisa de inúmeros fenômenos. Dominar essa linguagem te abrirá portas para diversas áreas, da engenharia à economia, da física à computação. Este guia, repleto de exercícios resolvidos, te fornecerá as ferramentas necessárias para não apenas entender, mas também dominar a arte da resolução de sistemas lineares, passo a passo, com clareza e precisão.
Prepare-se para desvendar os mistérios por trás das equações e transformar desafios em triunfos matemáticos!
Sistemas Lineares
Embarque conosco numa jornada fascinante pelo mundo dos sistemas lineares! Eles são a chave para desvendar inúmeros enigmas em diversas áreas do conhecimento, desde a engenharia e a economia até a biologia e a computação gráfica. Prepare-se para desvendar seus segredos e dominar sua resolução!
Sistemas lineares são um conjunto de equações lineares, onde cada equação representa uma reta em um espaço multidimensional. A solução do sistema, se existir, representa o ponto (ou pontos) de interseção entre essas retas. A beleza da linearidade reside em sua elegância e na possibilidade de aplicar métodos sistemáticos para encontrar soluções, mesmo em cenários complexos.
Definição e Aplicações de Sistemas Lineares
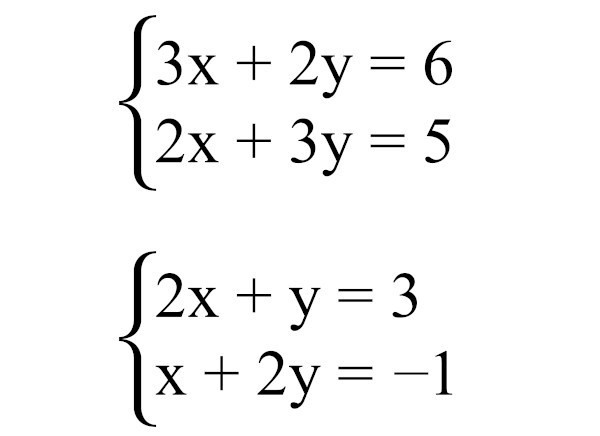
Um sistema linear é um conjunto de equações da forma a 1x 1 + a 2x 2 + … + a nx n = b, onde os a i são coeficientes constantes, os x i são as variáveis e b é um termo constante. Em um sistema de n equações com n incógnitas, buscamos os valores das variáveis que satisfazem simultaneamente todas as equações.
Por exemplo, em engenharia elétrica, sistemas lineares são usados para modelar circuitos elétricos, permitindo o cálculo das correntes e tensões em cada componente. Na economia, modelos de input-output, que descrevem a interdependência entre diferentes setores de uma economia, são representados por sistemas lineares. Na biologia, sistemas lineares podem modelar o crescimento populacional de espécies interagentes.
Sistemas Lineares Homogêneos e Não-Homogêneos

A distinção entre sistemas homogêneos e não-homogêneos reside no termo constante b. Em um sistema homogêneo, b é igual a zero em todas as equações (a 1x 1 + a 2x 2 + … + a nx n = 0). Sistemas homogêneos sempre possuem pelo menos uma solução trivial (x 1 = x 2 = …
= x n = 0). Já os sistemas não-homogêneos possuem pelo menos um b diferente de zero em alguma equação. Considere o sistema homogêneo: 2x + y = 0; x – y =
0. A solução trivial (x=0, y=0) é óbvia. Um exemplo de sistema não-homogêneo seria: 2x + y = 5; x – y = 1.
Aqui, a solução não é trivial e precisa ser encontrada através de métodos específicos.
Métodos de Resolução de Sistemas Lineares
Diversos métodos robustos existem para resolver sistemas lineares. O método de escalonamento (ou eliminação de Gauss) consiste em transformar o sistema em uma forma triangular superior, facilitando a obtenção da solução por substituição retroativa. Este método é eficiente e aplicável a sistemas de qualquer dimensão. A regra de Cramer, por sua vez, fornece uma solução explícita para sistemas quadrados (mesmo número de equações e incógnitas) com determinante da matriz dos coeficientes diferente de zero.
Embora elegante, a regra de Cramer torna-se computacionalmente custosa para sistemas de grande porte, sendo o escalonamento geralmente mais eficiente nestes casos.
Resolução de um Sistema Linear 3×3 pelo Método de Eliminação de Gauss
Vamos ilustrar a resolução de um sistema 3×3 usando o método de eliminação de Gauss. A eficiência deste método reside na sua capacidade de reduzir o sistema a uma forma mais simples, permitindo a resolução passo a passo. A organização em etapas facilita a compreensão e a verificação dos cálculos.
| Etapa | Operação | Matriz | Solução Parcial |
|---|---|---|---|
| 1 | Matriz original |
[ 1 2 -1 | 8 ] [ 2 -1 1 | 1 ] [ 1 -1 2 | 5 ] |
– |
| 2 | L2 = L2 – 2L1 L3 = L3 – L1 |
[ 1 2 -1 | 8 ] [ 0 -5 3 |-15] [ 0 -3 3 |-3 ] |
– |
| 3 | L3 = L3 – (3/5)L2 |
[ 1 2 -1 | 8 ] [ 0 -5 3 |-15] [ 0 0 6/5 | 6 ] |
– |
| 4 | Substituição retroativa (z=5, y=0, x=3) | – | x = 3, y = 0, z = 5 |
Matrizes e Sistemas Lineares: Os 10 Melhores Exercícios Sobre Sistemas Lineares Com O Gabarito! – Beduka

A álgebra linear, com sua elegância e poder, revela-se uma ferramenta essencial para decifrar os enigmas dos sistemas lineares. Através das matrizes, traduzimos a complexidade de equações em estruturas concisas e manipuláveis, abrindo caminho para soluções elegantes e eficientes.
Nesta jornada, exploraremos a intrincada relação entre matrizes e sistemas lineares, desvendando seus segredos e revelando sua beleza matemática.
A representação matricial de um sistema linear proporciona uma visão unificada e poderosa, simplificando a resolução e a análise. Essa representação permite a aplicação de métodos algébricos sofisticados, tornando a solução de sistemas complexos uma tarefa mais acessível.
Matriz Aumentada e seu Significado

Uma matriz aumentada é uma ferramenta fundamental na resolução de sistemas lineares. Ela combina a matriz de coeficientes do sistema com a matriz coluna dos termos independentes, fornecendo uma representação compacta e eficiente do sistema. Por exemplo, o sistema linear:
x + 2y = 5
3x – y = 1
pode ser representado pela matriz aumentada:
[ 1 2 | 5 ] [ 3 -1 | 1 ]
A linha vertical separa a matriz de coeficientes (à esquerda) do vetor dos termos independentes (à direita). Cada linha da matriz aumentada representa uma equação do sistema, e cada coluna representa os coeficientes de uma variável específica. A matriz aumentada facilita a aplicação de operações elementares de linha, que são cruciais para a resolução do sistema.
Operações Elementares de Linha e a Solução de Sistemas Lineares, Os 10 Melhores Exercícios Sobre Sistemas Lineares Com O Gabarito! – Beduka
As operações elementares de linha são transformações que preservam a solução do sistema linear. Essas operações incluem: trocar duas linhas, multiplicar uma linha por um escalar não nulo, e somar um múltiplo de uma linha a outra. A aplicação dessas operações à matriz aumentada permite a transformação do sistema em uma forma escalonada ou escalonada reduzida, facilitando a obtenção da solução.
Por exemplo, aplicando operações elementares de linha à matriz aumentada acima, podemos obter a forma escalonada reduzida, que diretamente nos fornece os valores de x e y que satisfazem o sistema. A manipulação estratégica dessas operações permite a resolução eficiente de sistemas, mesmo os mais complexos.
Matrizes Quadradas, Retangulares e suas Implicações na Resolução de Sistemas Lineares
Matrizes quadradas, com o mesmo número de linhas e colunas, possuem propriedades especiais que influenciam a resolução de sistemas lineares. Sistemas representados por matrizes quadradas com determinante diferente de zero possuem solução única. Já matrizes retangulares, com número diferente de linhas e colunas, levam a sistemas com solução única, infinitas soluções ou nenhuma solução, dependendo da relação entre o número de equações e o número de variáveis.
A análise da matriz, em particular seu posto, é crucial para determinar a natureza da solução. Sistemas com mais equações do que incógnitas podem ser inconsistentes (sem solução), enquanto sistemas com menos equações do que incógnitas podem ter infinitas soluções.
Determinante e o Número de Soluções de um Sistema Linear
A determinante de uma matriz quadrada desempenha um papel crucial na determinação do número de soluções de um sistema linear.
Um sistema linear representado por uma matriz quadrada de coeficientes possui:
- Solução única: se o determinante da matriz de coeficientes for diferente de zero.
- Infinitas soluções: se o determinante da matriz de coeficientes for zero e o sistema for consistente (ou seja, existe pelo menos uma solução).
- Nenhuma solução: se o determinante da matriz de coeficientes for zero e o sistema for inconsistente (ou seja, não existe solução).
Por exemplo:
- O sistema x + y = 2 e 2x + 2y = 4 tem matriz de coeficientes com determinante zero e infinitas soluções (pois as equações são linearmente dependentes).
- O sistema x + y = 2 e x + y = 3 tem matriz de coeficientes com determinante zero e nenhuma solução (pois as equações são inconsistentes).
- O sistema x + y = 2 e x – y = 0 tem matriz de coeficientes com determinante diferente de zero e uma única solução (x=1, y=1).

