Eu Preciso De Dois Exemplos De Equação Exponencial Com Gráfico: mergulhe no mundo das equações exponenciais e explore como elas moldam o nosso mundo. Essas equações, com suas características únicas, desempenham um papel fundamental em diversos campos, desde o crescimento populacional até o decaimento radioativo.
Neste artigo, vamos analisar dois exemplos de equações exponenciais, desvendando seus gráficos e as nuances que os tornam tão fascinantes.
As equações exponenciais são caracterizadas por um expoente variável, que determina o ritmo de crescimento ou decrescimento. O estudo dessas equações nos permite compreender como quantidades podem variar de forma acelerada ou gradual, revelando padrões que influenciam fenômenos da natureza, da economia e da ciência.
Equações Exponenciais: Uma Introdução aos Gráficos
Equações exponenciais são expressões matemáticas que envolvem uma variável no expoente. Elas descrevem o crescimento ou decaimento rápido de uma quantidade em relação a uma base constante. Essas equações são amplamente utilizadas em diversas áreas, como matemática, ciência, engenharia e finanças, para modelar fenômenos que envolvem crescimento ou decaimento exponencial.
Compreender o comportamento das funções exponenciais é fundamental para interpretar e prever o comportamento de sistemas que se desenvolvem de forma exponencial. As equações exponenciais nos permitem analisar e modelar fenômenos complexos, como o crescimento populacional, a propagação de doenças, o decaimento radioativo e o crescimento de investimentos.
Exemplos de Equações Exponenciais e seus Gráficos
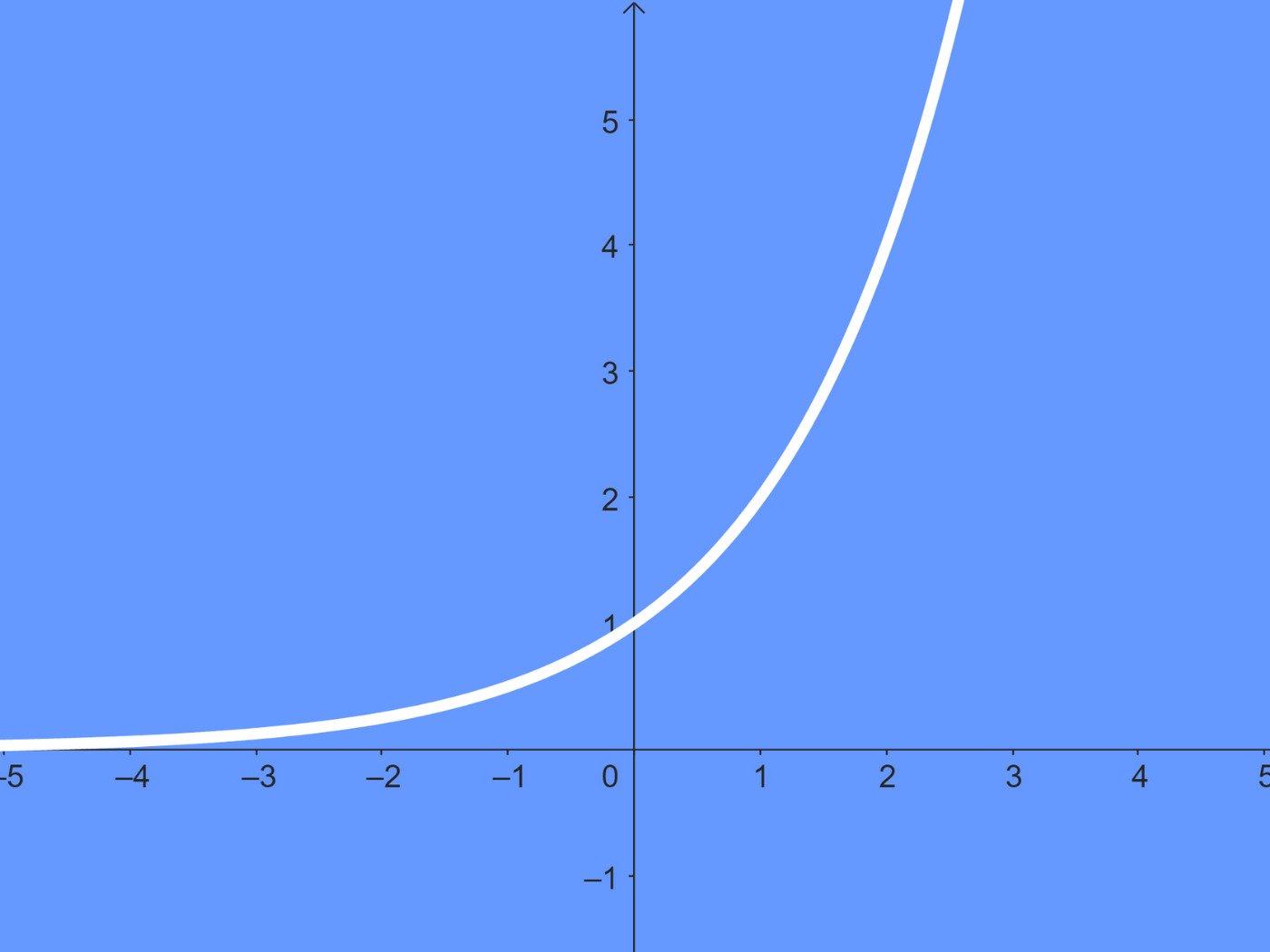
Para ilustrar o conceito de equações exponenciais, vamos analisar dois exemplos e seus respectivos gráficos:
| Equação 1 | Equação 2 | Gráfico da Equação 1 | Gráfico da Equação 2 |
|---|---|---|---|
| y = 2x | y = (1/2)x | [Gráfico da equação y = 2x, mostrando uma curva crescente que aumenta rapidamente à medida que x aumenta.] | [Gráfico da equação y = (1/2)x, mostrando uma curva decrescente que diminui rapidamente à medida que x aumenta.] |
A primeira equação, y = 2 x, representa uma função exponencial com base 2. O gráfico dessa função é uma curva crescente que aumenta rapidamente à medida que x aumenta. Isso ocorre porque a base é maior que 1. A segunda equação, y = (1/2) x, também é uma função exponencial, mas com base 1/2.
Seu gráfico é uma curva decrescente que diminui rapidamente à medida que x aumenta. Isso ocorre porque a base é menor que 1.
Análise dos Gráficos
Ao comparar os gráficos das duas equações exponenciais, podemos observar algumas diferenças importantes:
- A base da equação exponencial determina se o gráfico é crescente ou decrescente. Se a base é maior que 1, o gráfico é crescente, e se a base é menor que 1, o gráfico é decrescente.
- O expoente afeta a velocidade do crescimento ou decrescimento do gráfico. Quanto maior o expoente, mais rápido o gráfico cresce ou decresce.
Aplicações de Equações Exponenciais
As equações exponenciais são ferramentas poderosas para modelar e entender uma variedade de fenômenos em diferentes áreas, como:
- Crescimento Populacional:As equações exponenciais podem ser usadas para modelar o crescimento populacional de uma determinada região, considerando fatores como a taxa de natalidade, a taxa de mortalidade e a imigração.
- Investimentos Financeiros:No mundo financeiro, as equações exponenciais são usadas para calcular o crescimento de investimentos, como juros compostos. A fórmula do juros compostos é um exemplo clássico de equação exponencial.
- Modelagem de Doenças:As equações exponenciais podem ser usadas para modelar a propagação de doenças infecciosas, como a gripe ou o COVID-19, considerando a taxa de transmissão e o número de indivíduos infectados.
- Decaimento Radioativo:O decaimento radioativo de elementos instáveis também é modelado por equações exponenciais. Essas equações ajudam a determinar a meia-vida de um elemento radioativo, ou seja, o tempo necessário para que a quantidade de material radioativo seja reduzida pela metade.
Ao analisar os gráficos das equações exponenciais, notamos que a base da equação desempenha um papel crucial no comportamento do gráfico. Uma base maior implica em um crescimento mais rápido, enquanto uma base menor indica um crescimento mais lento. O expoente, por sua vez, determina a velocidade de crescimento ou decrescimento, revelando como a função evolui ao longo do tempo.
Compreender esses elementos é essencial para interpretar e aplicar as equações exponenciais em diversas áreas do conhecimento.
FAQ Guide: Eu Preciso De Dois Exemplos De Equação Exponencial Com Gráfico
O que é uma equação exponencial?
Uma equação exponencial é uma equação matemática onde a variável aparece no expoente. Por exemplo, 2^x = 8 é uma equação exponencial.
Qual a diferença entre uma equação exponencial e uma equação linear?
Em uma equação linear, a variável tem um expoente de 1. Em uma equação exponencial, a variável está no expoente.
Como posso resolver uma equação exponencial?
Existem vários métodos para resolver equações exponenciais, incluindo o uso de logaritmos, fatoração e substituição.

